Energy Vs Entropy: The Battle For The Control Wheel

Author: Arpan Dey

When we think of the universe, we are often reminded of a cold, dark and desolate stretch of spacetime, with tiny dots (galaxies) and even tinier dots (stars) trying their best to scream out their existence to the surrounding void. This picture might paint a universe that is devoid of much activity. However, a large portion of the matter in the universe is not in equilibrium [1]. If everything in the universe was in a state of perfect equilibrium, it would be as good as saying the universe does not exist. In fact, out of the many possible fates of the universe, one holds that over a long period of time, every part of the universe would reach a state of thermal equilibrium with every other part, meaning there would be no difference in temperature and energy between the different parts of the universe that could cause some changes to occur [2]. 

In their quest to understand the perplexities of the universe at all length scales, physicists have tried to identify and quantify potential fundamental parameters in terms of which a wide range of physical phenomena can be studied. Perhaps the two most important parameters in this regard are energy and entropy. Energy is that quantity that is usually minimized with time, as different processes evolve. More appropriately, with time the energy usually spreads out uniformly. Everything in the universe, broadly speaking, tends to reach an equilibrium state, which corresponds to minimum energy, or a state in which the energy is evenly distributed in the entire system. This simple idea can explain a lot of changes we see in the world around us: in many cases, the systems undergo these changes to effectively lose energy to its surroundings and reach a stable, equilibrium state. Studying the world through the lens of energy has proved to be a time-tested and effective method. However, another significant player here, which overrides energy in importance for certain processes, is entropy.

The concept of entropy is one of the most fundamental concepts in physics. Usually it is said that the more the disorder, the more the entropy. However, this simple definition of entropy can be deceptive without a deeper understanding. As per the second law of thermodynamics, the entropy of a closed system must always either remain the same or increase. This is why any machine must always waste some energy on its functioning and become less efficient over time. The idea of a perpetual motion machine is not just an engineering problem – it is prohibited by the laws of physics. For a perpetual motion machine to exist, the machine must be able to generate energy without external work. In other words, connecting back to our discussion on energy, the machine should, all by itself, refuse to reach an equilibrium state and continue operating. Of course, this claim is absurd, both theoretically and practically. 

Entropy can be defined as the number of ways a particular state can be achieved. This does not mean just the number of ways the different parts of a system can be arranged (spatial configurations). We also have to take into account the velocities and energies of all the parts of the system at a given point in time. In our universe, it is clear that entropy is increasing with time. It might seem that the entropy increases in our universe because the universe is expanding and more and more spatial configurations become possible within the volume of the universe due to the expansion. However, as discussed, entropy does not depend solely on the number of different spatial configurations possible. Even if the universe were contracting, the overall entropy might have increased due to the fact that every object in the universe could emit radiation, which contains energy, thus increasing the number of possible energy configurations of the universe, since the radiation (or photons) would spread throughout the universe and disperse its energy everywhere. 

So, in our universe, entropy always increases. Even if we forcibly try to prevent a system from reaching equilibrium (the highest entropy state), we must be aware of the states of the particles to achieve this feat. Here, the information of the states in our brains can be thought of as a factor that contributes to the increase of the overall entropy. And even if we try to forget this information, the temperature around our brain increases, thus not letting entropy to decrease!

Figure 1: Entropy increases as a system evolves from an ordered state to a disordered state.

The concept of entropy is believed by many to be responsible for the unidirectional flow of time. Why does time not run backward? It is a great puzzle that the laws of physics make no distinction between the past and the future - meaning it is theoretically possible for time to "run backward" - yet we don’t see a broken cup pick itself up from the floor and repair itself. Ludwig Boltzmann assumed that our universe began in a very unlikely state. Entropy increases both into the past and the future, and we are existing on the lower vertex of a ‘V’-shaped function on an entropy-time graph. Our universe, Boltzmann argued, could have come into existence just a moment ago, complete with "false memories" of a past that never really occurred. Indeed, there is a small but non-zero chance that some gas molecules in an open container do not come out of it even when the surroundings are devoid of any gas molecules. This does not generally happen, for everything will tend to achieve an equilibrium with the surroundings. But if we wait long enough, such things must occur, simply because there is a non-zero probability for them to occur, no matter how small. Given enough time, we may see some atoms in a system huddle in a corner of the system all by themselves and not move. In such cases, as the system was in a more likely state before this new state was achieved, entropy also increases into the past. Over a sufficiently long time, transitions from a likely state (a disordered or high-entropy state) to a less-likely (more ordered) state become possible, and probably such a fluctuation is responsible for the creation of the world around us. However, asked Boltzmann, isn’t it more likely that a single brain spontaneously self-assembled with false memories of the universe, rather than the entire universe – with all its structures – spontaneously emerging? Statistically speaking, it might be more likely for a brain to spontaneously emerge out of nowhere, complete with false memories of the universe, than for the universe to exist physically. This is the "Boltzmann brain" hypothesis [3], and although there are some flaws with this argument, it is still a mind-bending thought experiment that exposes many fundamental limitations in our theories that are often swept under the rug.

Now, let us try to properly define entropy. We may define entropy as a measure of disorder in a non-technical fashion, but that is not exactly so. A common scenario often employed to illustrate the idea of entropy is that if you have an untidy room, it's in a high entropy state, whereas a neat and clean room will have a low entropy. That's true, but not a very accurate description of the concept of entropy. Let us consider a better example, even at the cost of the simplicity of the previous illustration. If we have five differently colored balls and two boxes, the lowest entropy state would be achieved if we keep all five balls in one box and thus, no balls in the other. There are only two ways we can achieve this configuration: either put all the balls in the first box keeping the second box empty, or vice versa. This indicates low entropy. Also, this state is clearly not an equilibrium configuration, because the "concentration" of the balls is higher on one side. If we decide to keep two balls in one box and three in the other, by taking into account the five different colors, the number of ways we can achieve this state goes up drastically, indicating a higher entropy. And in this case, a near-equilibrium is attained. This is a beautiful illustration of how increasing entropy corresponds to the system moving toward equilibrium. 

Thus, both energy and entropy seem to be fundamental driving factors that determine the evolution of various processes that occur in the universe. Every change tends to minimize energy. Also, every change tends to maximize the overall entropy of the universe. Are these two statements equivalent? Or is energy more fundamental than entropy? Or does entropy get access to the ultimate control wheel that drives various processes in the universe?

The most likely answer is: both energy and entropy are on the same footing, but depending on the particular system or process, one might play a more dominant role than the other. Let us consider a simple example. Consider Brownian motion [4]: the random motion of particles in a medium due to collision with the particles of the medium. Brownian motion can be understood in terms of energy or entropy. The collisions, which are of a random nature, ensure a constant exchange of kinetic energy between the particles, and the system is in a state of thermal equilibrium, because the energy is evenly distributed throughout the system. In terms of entropy, the constant and random collisions between the particles takes the system to the most disordered and random state, indicating maximum entropy. Let us consider another illustration: the mixing of two different gases. If we initially keep the gases separated within a container, the gases will inevitably mix over time. The initial configuration was a low-entropy state. When the gases have perfectly mixed with each other, the system has reached an equilibrium configuration and its entropy is maximized. Does this mean the maximum entropy state is always achieved when two samples are mixed? Not quite. Let us consider a final example. 

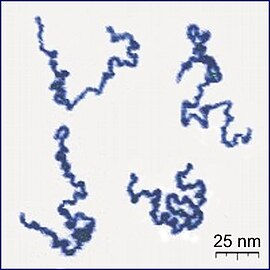
Polymers are connected chains of smaller chemical units. Polymers form an integral part of many essential components that comprise living organisms, and hence are of significant interest to biologists. When two polymer chains are kept in a mixed state in a confined volume, they are often found to spontaneously separate [5]. Given the physical dimension of polymers, one might expect them to exhibit Brownian motion, but polymers do not always mix. According to researchers, the primary reason behind this is that polymers try to minimize the free energy, which is defined as U - TS, where U is the internal energy, T is the temperature and S is the entropy of the system. The minimization of free energy is achieved through subtle changes in the internal energy U and the entropy S. From the equation for free energy, U - TS, it is clear that entropy will play a more dominant role at higher temperatures. The crucial difference between the system of gas molecules and the polymers is that gas molecules are free particles, whereas the polymers are connected chains. If the polymers are mixed and kept in a confined volume, they cannot effectively vibrate, leading to a decrease in the number of possible configurations, and hence a decrease in entropy. On the other hand, if within the same confined volume the polymers are separate, they can vibrate more freely, indicating a higher number of possible configurations and a higher entropy. This is a beautiful illustration of how studying the world around us through the lens of energy and entropy might shed light on many perplexing and counterintuitive phenomena. 

Figure 2: Linear polymer chains suspended in a liquid medium, observed under a microscope (Source: Wikipedia)

Indeed, the very fact that we have been able to identify parameters like energy and entropy that can explain so much is surprising in its own right. But what is perhaps even more exciting is how much more of the universe we can explore and understand. The intricate dance between parameters like energy and entropy keeps the wheels of the universe rolling, with energy taking the driver’s seat for certain phenomena and entropy for others. And even though the universe might be headed for that uninteresting equilibrium state we discussed - where nothing can occur anymore, it is still true that if it was not for energy and entropy, you would not be reading this right now!

References

[1] Ethan Siegel. Be thankful for an out-of-equilibrium Universe. Big Think. 2022. https://bigthink.com/starts-with-a-bang/thankful-out-of-equilibrium/ 

[2] NASA/WMAP Science Team. What is the Ultimate Fate of the Universe? 2014. https://wmap.gsfc.nasa.gov/universe/uni_fate.html 

[3] Jason Segall, Graeme Ackland. The Boltzmann Brain. Higgs Centre for Theoretical Physics, The University of Edinburgh. https://higgs.ph.ed.ac.uk/outreach/higgshalloween-2021/boltzmann-brain

[4] Anne Marie Helmenstine. An Introduction to Brownian Motion. ThoughtCo. 2023. https://thoughtco.com/brownian-motion-definition-and-explanation-4134272 

[5] Silvia Moreno Pinilla. Polymers in Solution. Leibniz Institute of Polymer Research Dresden. 2020. https://www.ipfdd.de/fileadmin/user_upload/rp/Moreno/Polymers_in_solution_TU2020_Lecture3_2.pdf